tak ada kata yang pantas terucap untukmu ayah. Mungkin engkau bukan orang terdekat. Mungkin engkau juga bukan yang selalu berada disampingku, saat aku bahagia, kecewa bahkan saat aku bersedih hingga meneteskan air mata.
Saat anak-anak pergi sekolah dengan ayahnya yang juga pergi bekerja, kita tidak pernah melakukanya karena kau yang harus berangkat lebih dulu saat matahari belum menampakan cahayanya.
Saat anak-anak menunggu kepulangan ayahnya untuk bermain bersama, tidak dengan aku yang selalu terlelap saat menunggu kepulanganmu yang begitu larut. Andai dapat ku beli waktu kerjamu kala itu, aku rela membayarnya dengan uang jajanku untuk bisa bermain bersamamu.
Kita mungkin bukan pasangan yang baik. Kau sibuk dengan urusanmu, sedangkan aku bermain dengan semua khayalanku.
Saat aku mulai tumbuh besar, kita mulai punya waktu untuk bersama. Tapi bukan untuk bermain melainkan melakukan pekerjaan yang tidak aku inginkan. Seolah kau menindasku, aku jadi tidak suka denganmu. Aku membenci semua tentangmu. Kau marahi aku jika melakukan pekerjaan yang tidak sesuai dengan maumu. Kau buat aku merasa lemah dengan ucapan-ucapan kasarmu. Ingin rasanya kau segera tiada dari duniaku, mengakhiri semua penderitaan dalam kehidupanku.
Pernah sekali aku menyalahkanmu atas apa yang terjadi dalam hidupku. Kusadari kau menangis saat ku terbangun sejenak dari tidur lelapku. Lama setelah itu, kupandangi wajahmu saat tertidur lelap, terbayang kerja keras yang kau lakukan untuk membesarkanku. Terbayang letih yang tersimpan dalam dirimu atas kerja keras yang kau lakukan untuk memenuhi kebutuhanku. Seakan tak tahu apa jadinya diri ini jika tanpa kehadiranmu. Tak ingin rasanya kehilanganmu dari sisiku.
Kini aku telah dewasa. Tumbuh menjadi seorang pemuda mandiri yang juga tidak dapat melupakan kasih sayang keluarganya. Kau ajarkan aku menjadi seorang yang siap menjalani kerasnya hidup tanpa melupakan kelembutan hati. Kau ajarkan padaku bagaimana menjadi pribadi yang kuat tanpa melupakan setiap orang punya kelemahan. Kau tanamkan padaku mencapai keberhasilan tanpa melupakan kalau setiap orang pasti pernah mengalami kegagalan. Kau buat aku berdiri di jalan yang penuh dengan hambatan dan rintangan agarku dapat menaklukan kerasnya kehidupan. Kau jadikan aku sebagai seorang pemimpin yang sanggup memimpin dirinya sebelum mempunyai kesempatan untuk memimpin orang lain. Dan yang jauh lebih penting dari itu semua adalah kau membuat aku merasa bangga atas semua yang telah kau lakukan untukku.
Karena itulah, aku selalu berdoa ”semoga Tuhan selalu memberi yang terbaik untukmu”
Untuk setiap detak yang terjadi dalam nadi dan jantungku, hatiku berkata ”Terima Kasih Ayah”
Sabtu, 26 November 2011
manajemen wkatu dalam islam
Orang yang akan melakukan perjalanan jauh pasti akan menyiapkan perbekalan yang cukup. Lihatlah misalnya orang yang hendak menunaikan ibadah haji. Terkadang ia mengumpulkan harta dan perbekalan sekian tahun lamanya. Padahal itu berlangsung sebentar, hanya beberapa hari saja. Maka mengapa untuk suatu perjalanan yang tidak pernah ada akhirnya –yakni perjalanan akhirat- kita tidak berbekal diri dengan ketaatan ?! Padahal kita yakin bahwa kehidupan dunia hanyalah bagaikan tempat penyeberangan untuk sampai kehidupan yang kekal nan abadi yaitu kehidupan akhirat. Di mana manusia terbagi menjadi: ashabul jannah (penghuni surga) dan ashabul jahim (penghuni neraka). Itulah hakikat perjalananmanusiaa di dunia ini. Maka sudah semestinya kita mengisi waktu dna sisa umur yang ada dengan berbekal amal kebaikan untuk menghadapi kehidupan yang panjang. Allah berfirman yang artinya:
“Hai orang-orang yang beriman, bertakwalah kepada Allah dan hendaklah setiap diri memperhatikan apa yang telah diperbuatnya untuk hari esok (akhirat), dan bertakwalah kepada Allah, sesungguhnya Allah Maha Mengetahui apa yang kamu kerjakan.” (QS. Al-Hasyr’: 18)
Ibnu Katsir rahimahullah berkata,
“Hisablah diri kalian sebelum dihisab, perhatikanlah apa yang sudah kalian simpan dari amal shalih untuk hari kebangkitan serta (yang akan) dipaparkan kepada Rabb kalian.” (Taisir Al-‘Aliyil Qadir, 4/339)
Umur Bukan Pemberian Cuma-Cuma
“Hai orang-orang yang beriman, bertakwalah kepada Allah dan hendaklah setiap diri memperhatikan apa yang telah diperbuatnya untuk hari esok (akhirat), dan bertakwalah kepada Allah, sesungguhnya Allah Maha Mengetahui apa yang kamu kerjakan.” (QS. Al-Hasyr’: 18)
Ibnu Katsir rahimahullah berkata,
“Hisablah diri kalian sebelum dihisab, perhatikanlah apa yang sudah kalian simpan dari amal shalih untuk hari kebangkitan serta (yang akan) dipaparkan kepada Rabb kalian.” (Taisir Al-‘Aliyil Qadir, 4/339)
Umur Bukan Pemberian Cuma-Cuma
Waktu adalah sesuatu yang terpenting untuk diperhatikan. Jika ia berlalu tak akan kembali. Setiap hari dari waktu kta berlalu, berarti ajal semakin dekat. Umur merupakan nikmat yang seseorang akan ditanya tentangnya. Nabi bersabda yang artinya: “Tidak akan bergeser kaki manusia di hari kiamat dari sisi Rabbnya sehingga ditanya tentang lima hal: tentang umurnya dalam apa ia gunakan, tentang masa mudanya dalam apa ia habiskan, tentang hartanya darimana ia peroleh dan dalam hal apa ia belanjakan, dan tentang apa yang ia amalkan dari yang ia ketahui (ilmu).”
(HR. At-Tirmidzi dari jalan Ibnu Mas’ud radliyallahu anha. Lihat Ash-Shahihah, no. 946)
Jangan Menunda-nunda Beramal
(HR. At-Tirmidzi dari jalan Ibnu Mas’ud radliyallahu anha. Lihat Ash-Shahihah, no. 946)
Jangan Menunda-nunda Beramal
Mungkin kita sering mendengar orang mengatakan:
“Mumpung masih muda kita puas-puaskan berbuat maksiat, gampang kalau sudah tua kita sadar.” Sungguh betapa kejinya ucapan ini. Apakah dia tahu kalau umurnya akan panjang ? Kalau seandainya dia ditakdirkan panjang, apa ada jaminan dia akan sadar ? Atau justru akan bertambah kesesatannya ?! Allah berfirman yang artinya:
“Dan tiada yang dapat mengetahui (dengan pasti) apa yang akan diusahakannya besok. Dan tiada seorang pun yang dapat mengetahui di bumi mana dia akan mati. Sesungguhnya Allah Maha Mengetahui lagi Maha Mengenal.”
(QS. Luqman: 34)
Ibnul Qayyim rahimahullah berkata:
“Sesungguhnya angan-angan adalah modal utama orang-orang yang bangkrut.” (Ma’alim fi Thariqi ‘Ilmi hal. 32)
“Apabila engkau berada di waktu sore janganlah menunggu (menunda beramal) di waktu pagi. Dan jika berada di waktu pagi , janganlah menunda (beramal) di waktu sore. Gunakanlah masa sehatmu untuk masa sakitmu dan kesempatan hidupmu untuk saat kematianmu.” (HR. Al-Bukhari no. 6416)
Selagi kesempatan masih diberikan, jangan menunda-nunda lagi. Akankah seseorang menunda hingga apabila ajal menjemput, betis bertaut dengan betis, sementara lisanpun telah kaku dan tubuh tidak bisa lagi digerakkan ? Dan ia pun menyesali umur yang telah dilalui tanpa bekal untuk suatu kehidupan yang panjang ?! Allah berfirman menjelaskan penyesalan orang-orang kafir ketika datang kematian.
“Dan tiada yang dapat mengetahui (dengan pasti) apa yang akan diusahakannya besok. Dan tiada seorang pun yang dapat mengetahui di bumi mana dia akan mati. Sesungguhnya Allah Maha Mengetahui lagi Maha Mengenal.”
(QS. Luqman: 34)
Ibnul Qayyim rahimahullah berkata:
“Sesungguhnya angan-angan adalah modal utama orang-orang yang bangkrut.” (Ma’alim fi Thariqi ‘Ilmi hal. 32)
“Apabila engkau berada di waktu sore janganlah menunggu (menunda beramal) di waktu pagi. Dan jika berada di waktu pagi , janganlah menunda (beramal) di waktu sore. Gunakanlah masa sehatmu untuk masa sakitmu dan kesempatan hidupmu untuk saat kematianmu.” (HR. Al-Bukhari no. 6416)
Selagi kesempatan masih diberikan, jangan menunda-nunda lagi. Akankah seseorang menunda hingga apabila ajal menjemput, betis bertaut dengan betis, sementara lisanpun telah kaku dan tubuh tidak bisa lagi digerakkan ? Dan ia pun menyesali umur yang telah dilalui tanpa bekal untuk suatu kehidupan yang panjang ?! Allah berfirman menjelaskan penyesalan orang-orang kafir ketika datang kematian.
“(Demikianlah keadaan orang-orang kafir itu), hingga apabila datang kematian kepada seorang dari mereka, dia berkata: ‘Ya Rabbku, kembalikanlah aku (ke dunia), agar aku berbuat amal yang shalih terhadap apa yang telah aku tinggalkan. ‘Sekali-kali tidak. Sesungguhnya itu adalah perkataan yang diucapkannya saja.” (QS. Al-Mu’minun: 99-100) Umur Umat Ini
Allah telah menakdirkan bahwa umur umat ini tidak sepanjang umur umat terdahulu. Yang demikian mengandung hikmah yang terkadang tidak diketahui oleh hamba. Nabi bersabda dalam hadits yang diriwayatkan oleh At-Tirmidzi dari sahabat Abu Hurairah:
“Umur-umur umatku antara 60 hingga 70, dan sedikit dari mereka yang melebihi itu.” (Dihasankan sanadnya oleh Ibnu Hajar rahimahullah dalam Fathul Bari, 11/240) Maksud dari hadits ini adalah bahwa keumuman ajal umat ini antara umur 60 hingga 70 tahun. Dengan bukti keadaan yang bisa disaksikan. Di mana di antara umat ini ada yang (mati) sebelum mencapai umur 60 tahun. Ini termasuk dari rahmat Allah dan kasih sayang-Nya supaya umat ini tidak terlibat dengan kehidupan dunia kecuali sebentar. Karena umur, badan, dan rizki umat-umat terdahulu lebih besar sekian kali lipat dibandingkan umat ini.
Dahulu ada yang diberi umur hingga seribu tahun, panjang tubuhnya mencapai lebih dari 80 hasta atau kurang. Satu biji gandum besarnya seperti pinggang sapi. Satu delima diangkat oleh sepuluh orang. Mereka mengambil dari kehidupan dunia sesuai dengan jasad dan umur mereka. Namun mereka sombong dan berpaling dari Allah. Sehingga manusia pun terus mengalami penurunan bentuk fisik, rizki, dan ajal.
maka manfaatkanlah sisa usia kita di jalan allah ‘azza wa jalla dengan memberantas kesyirikan di bumi ini dengan mengorbankan jiwa dan harta kita,Sehingga umat ini menjadi umat yang terakhir. Yang mengambil rizki sedikit dengan badan yang lemah dan pada masa yang pendek, mengambil jizyah dan atau ghanimah dan fa’i dari orang orang kafir yang hina. Supaya mereka tidak menyombongkan diri, dan hanya allah saja lah yang berhaq di ibadahi. maka untuk apa lagi kita menunda dan menanti untuk ‘amaliyat, sedangkan umur terus bertambah dan kematian tak terhindarkan. semoga allah ta’ala memberi karunia dan rahmat Nya kepada kita… dan ‘amaliyat kita diterima sehingga kita tergolong dalam golongan para syuhada….Amin
Dahulu ada yang diberi umur hingga seribu tahun, panjang tubuhnya mencapai lebih dari 80 hasta atau kurang. Satu biji gandum besarnya seperti pinggang sapi. Satu delima diangkat oleh sepuluh orang. Mereka mengambil dari kehidupan dunia sesuai dengan jasad dan umur mereka. Namun mereka sombong dan berpaling dari Allah. Sehingga manusia pun terus mengalami penurunan bentuk fisik, rizki, dan ajal.
maka manfaatkanlah sisa usia kita di jalan allah ‘azza wa jalla dengan memberantas kesyirikan di bumi ini dengan mengorbankan jiwa dan harta kita,Sehingga umat ini menjadi umat yang terakhir. Yang mengambil rizki sedikit dengan badan yang lemah dan pada masa yang pendek, mengambil jizyah dan atau ghanimah dan fa’i dari orang orang kafir yang hina. Supaya mereka tidak menyombongkan diri, dan hanya allah saja lah yang berhaq di ibadahi. maka untuk apa lagi kita menunda dan menanti untuk ‘amaliyat, sedangkan umur terus bertambah dan kematian tak terhindarkan. semoga allah ta’ala memberi karunia dan rahmat Nya kepada kita… dan ‘amaliyat kita diterima sehingga kita tergolong dalam golongan para syuhada….Amin
wallahu ta’ala a’lam bis showab..
perkembangan sistem bilangan
Benda Sebagai Representasi Bilangan
Sejarah perkembangan sistem bilangan berawal dari zaman Paleolitikum atau zaman batu tua sekitar 30.000 tahun yang lalu. Tanda yang digunakan untuk mewakili suatu angka pada zaman tersebut yakni irisan-irisan atau ukiran yang digoreskan pada dinding gua atau pada tulang, kayu, atau batu. Satu irisan menandakan satu benda, oleh karena itu sepuluh rusa kutub ditandai oleh sepuluh ukiran. Banyaknya tanda berkorespondensi satu-satu dengan banyaknya benda yang dihitung. Karena sistem yang digunakan sangat tidak praktis untuk mewakili suatu angka, di Persia, pada abad kelima sebelum masehi, terjadi suatu perkembangan sistem bilangan yakni dengan digunakannya simpul-simpul yang disusun pada tali. Pada abad ketiga belas, suku Inca menggunakan sistem yang sama dengan mengembangkan quipu, suatu tali yang disusun secara horizontal dimana dari tali tersebut digantung berbagai macam benang. Jenis simpul yang digunakan, panjang dari tali, dan warna serta posisi benang menandakan tingkatan kuantitas: satuan, puluhan, dan ratusan. Beberapa peradaban juga menggunakan sistem bilangan untuk merepresentasikan banyaknya obyek yang berbeda-beda yakni dengan menggunakan berbagai macam bebatuan, seperti bangsa Sumeria yang menggunakan batu tanah liat yang disebut calculi – bahasa latin dari calculi yakni calculus. Tanah liat bangsa Sumeria tersebut digunakan pada abad keempat sebelum masehi. Batu tanah liat kecil yang berbentuk kerucut mewakili banyaknya satu obyek, yang berbentuk bola mewakili banyaknya sepuluh, dan batu tanah liat besar yang berbentuk kerucut mewakili enam puluh.
Sejarah perkembangan sistem bilangan berawal dari zaman Paleolitikum atau zaman batu tua sekitar 30.000 tahun yang lalu. Tanda yang digunakan untuk mewakili suatu angka pada zaman tersebut yakni irisan-irisan atau ukiran yang digoreskan pada dinding gua atau pada tulang, kayu, atau batu. Satu irisan menandakan satu benda, oleh karena itu sepuluh rusa kutub ditandai oleh sepuluh ukiran. Banyaknya tanda berkorespondensi satu-satu dengan banyaknya benda yang dihitung. Karena sistem yang digunakan sangat tidak praktis untuk mewakili suatu angka, di Persia, pada abad kelima sebelum masehi, terjadi suatu perkembangan sistem bilangan yakni dengan digunakannya simpul-simpul yang disusun pada tali. Pada abad ketiga belas, suku Inca menggunakan sistem yang sama dengan mengembangkan quipu, suatu tali yang disusun secara horizontal dimana dari tali tersebut digantung berbagai macam benang. Jenis simpul yang digunakan, panjang dari tali, dan warna serta posisi benang menandakan tingkatan kuantitas: satuan, puluhan, dan ratusan. Beberapa peradaban juga menggunakan sistem bilangan untuk merepresentasikan banyaknya obyek yang berbeda-beda yakni dengan menggunakan berbagai macam bebatuan, seperti bangsa Sumeria yang menggunakan batu tanah liat yang disebut calculi – bahasa latin dari calculi yakni calculus. Tanah liat bangsa Sumeria tersebut digunakan pada abad keempat sebelum masehi. Batu tanah liat kecil yang berbentuk kerucut mewakili banyaknya satu obyek, yang berbentuk bola mewakili banyaknya sepuluh, dan batu tanah liat besar yang berbentuk kerucut mewakili enam puluh.
Penemuan Angka
Penulisan symbol matematika pertama muncul di zaman Babylonia (sekitar 3300 sebelum masehi). Mereka menulis atau menggambar bentuk paku untuk mewakili satu, sedangkan bentuk V mewakili sepuluh. Sembilan paku dan satu V berarti sembilan belas. Zaman berkembang dan melahirkan berbagai peradaban yang juga menggunakan sistem bilangan yang sama dengan bangsa Babylonia. Bangsa Maya misalnya menggunakan garis sebagai representasi dari angka lima dan titik yang mewakili angka satu. Mereka menuliskan 19 dengan tiga garis dan empat titik. Bangsa Mesir kuno menggunakan garis untuk mewakili satuan, bentuk pegangan keranjang untuk puluhan, bentuk gulungan tali untuk ratusan, dan bentuk bunga lotus untuk mewakili ribuan. Sistem bilangan tersebut adalah contoh sistem bilangan penjumlahan, karena nilai dari suatu angka sama dengan jumlah nilai dari simbol yang mewakilinya. Bangsa Romawi yang menemukan sistem biilangan Romawi juga dianggap sebagai sistem bilangan penjumlahan. Misalnya XI berarti 10 + 1 = 11. Keunggulan dari sistem bilangan romawi ini yakni, apabila menempatkan angka yang lebih kecil di depan sebelum bilangan yang lebih besar maka akan menandakan pengurangan misalnya IX berarti 10 – 1 = 9.
Penulisan symbol matematika pertama muncul di zaman Babylonia (sekitar 3300 sebelum masehi). Mereka menulis atau menggambar bentuk paku untuk mewakili satu, sedangkan bentuk V mewakili sepuluh. Sembilan paku dan satu V berarti sembilan belas. Zaman berkembang dan melahirkan berbagai peradaban yang juga menggunakan sistem bilangan yang sama dengan bangsa Babylonia. Bangsa Maya misalnya menggunakan garis sebagai representasi dari angka lima dan titik yang mewakili angka satu. Mereka menuliskan 19 dengan tiga garis dan empat titik. Bangsa Mesir kuno menggunakan garis untuk mewakili satuan, bentuk pegangan keranjang untuk puluhan, bentuk gulungan tali untuk ratusan, dan bentuk bunga lotus untuk mewakili ribuan. Sistem bilangan tersebut adalah contoh sistem bilangan penjumlahan, karena nilai dari suatu angka sama dengan jumlah nilai dari simbol yang mewakilinya. Bangsa Romawi yang menemukan sistem biilangan Romawi juga dianggap sebagai sistem bilangan penjumlahan. Misalnya XI berarti 10 + 1 = 11. Keunggulan dari sistem bilangan romawi ini yakni, apabila menempatkan angka yang lebih kecil di depan sebelum bilangan yang lebih besar maka akan menandakan pengurangan misalnya IX berarti 10 – 1 = 9.
Penemuan Sistem Nilai Tempat
Pada sistem bilangan yang telah dituliskan di atas, nilai digit hanya mempunyai sedikit hubungan bahkan tidak sama sekali terhadap posisi di mana mereka dituliskan. Bahkan, pada sistem bilangan romawi, meski penempatan tertentu dapat bermakna pengurangan. I tetap berarti satu meski ditempatkan sebelum atau sesudah X. C selalu bernilai seratus dimanapun posisinya dituliskan; MCI berarti seribu seratus satu.
Bilangan yang bergantung pada tempat yang merupakan ciri khas dari sistem bilangan sekarang merupakan gagasan penting pada evolusi sistem bilangan. Ide dari sistem bilangan tersebut menggunakan sistem perkalian. Contohnya yakni digit 2 pada kolom kedua dari kiri menandakan dua kali sepuluh, tetapi apabila ditempatkan pada kolom ketiga dari kiri berarti dua kali seratus. Bilangan 1 sampai 9 muncul di India pada prasasti-prasasti di abad ke-13, namun ide dari angka 0 pada saat itu belum ditemukan. Gabungan angka yang bergantung tempat dan ide dari angka 0 di India pada abad kelima setelah masehi, dalam perjalanannya dari Arab ke Eropa, menghasilkan sistem bilangan baru yang handal. Sistem yang membawa kemajuan dalam perhitungan dan perkembangan matematika modern. Pada abad ke-9, seorang matematikawan Persia, Muhammad Ibn Musa al-Khwarismi menulis suatu buku yang berjudul “Buku Penjumlahan dan Pengurangan dengan Cara Bangsa India” melahirkan ide baru. Buku tersebut menjadi terkenal di Eropa dan selanjutnya diterjemahkan ke bahasa Latin pada abad ke-12 yang melahirkan kolom aritmetika, yakni menggunakan sistem simpan dan pinjam pada metode perhitungan. Dari waktu ke waktu kolom aritmetika dikenal sebagai algorism – nama latin dari al-Khwarismi. Dan sekarang ini, kita menggunakan istilah algoritma.
Pada sistem bilangan yang telah dituliskan di atas, nilai digit hanya mempunyai sedikit hubungan bahkan tidak sama sekali terhadap posisi di mana mereka dituliskan. Bahkan, pada sistem bilangan romawi, meski penempatan tertentu dapat bermakna pengurangan. I tetap berarti satu meski ditempatkan sebelum atau sesudah X. C selalu bernilai seratus dimanapun posisinya dituliskan; MCI berarti seribu seratus satu.
Bilangan yang bergantung pada tempat yang merupakan ciri khas dari sistem bilangan sekarang merupakan gagasan penting pada evolusi sistem bilangan. Ide dari sistem bilangan tersebut menggunakan sistem perkalian. Contohnya yakni digit 2 pada kolom kedua dari kiri menandakan dua kali sepuluh, tetapi apabila ditempatkan pada kolom ketiga dari kiri berarti dua kali seratus. Bilangan 1 sampai 9 muncul di India pada prasasti-prasasti di abad ke-13, namun ide dari angka 0 pada saat itu belum ditemukan. Gabungan angka yang bergantung tempat dan ide dari angka 0 di India pada abad kelima setelah masehi, dalam perjalanannya dari Arab ke Eropa, menghasilkan sistem bilangan baru yang handal. Sistem yang membawa kemajuan dalam perhitungan dan perkembangan matematika modern. Pada abad ke-9, seorang matematikawan Persia, Muhammad Ibn Musa al-Khwarismi menulis suatu buku yang berjudul “Buku Penjumlahan dan Pengurangan dengan Cara Bangsa India” melahirkan ide baru. Buku tersebut menjadi terkenal di Eropa dan selanjutnya diterjemahkan ke bahasa Latin pada abad ke-12 yang melahirkan kolom aritmetika, yakni menggunakan sistem simpan dan pinjam pada metode perhitungan. Dari waktu ke waktu kolom aritmetika dikenal sebagai algorism – nama latin dari al-Khwarismi. Dan sekarang ini, kita menggunakan istilah algoritma.
perkembangan logika matematika
Sejarah Singkat dan Perkembangan Logika
Dasar dari logika adalah penalaran, sejak manusia ada di dunia ini, manusia telah menggunakan akal pikirannya untuk menarik sebuah kesimpulan ataupun penalaran Logika berasal dari kata Yunani kuno λόγος (logos) yang berarti hasil pertimbangan akal pikiran yang diutarakan lewat kata dan dinyatakan dalam bahasa. Sebagai ilmu, logika disebut dengan logike episteme (Latin: logica scientia) atau ilmu logika (ilmu pengetahuan) yang mempelajari kecakapan untuk berpikir secara lurus, tepat, dan teratur
Masa Yunani Kuno, logika dimulai sejak Thales (624 SM - 548 SM), filsuf Yunani pertama yang meninggalkan segala dongeng, takhayul, dan cerita-cerita isapan jempol dan berpaling kepada akal budi untuk memecahkan rahasia alam semesta.
Thales mengatakan bahwa air adalah arkhe (Yunani) yang berarti prinsip atau asas utama alam semesta. Saat itu Thales telah mengenalkan logika induktif.
Aristoteles kemudian mengenalkan logika sebagai ilmu, yang kemudian disebut logica scientica. Aristoteles mengatakan bahwa Thales menarik kesimpulan bahwa air adalah arkhe alam semesta dengan alasan bahwa air adalah jiwa segala sesuatu.
Dalam logika Thales, air adalah arkhe alam semesta, yang menurut Aristoteles disimpulkan dari:
* Air adalah jiwa tumbuh-tumbuhan (karena tanpa air tumbuhan mati)
* Air adalah jiwa hewan dan jiwa manusia
* Air jugalah uap
* Air jugalah es
Jadi, air adalah jiwa dari segala sesuatu, yang berarti, air adalah arkhe alam semesta.
Sejak saat Thales sang filsuf mengenalkan pernyataannya, logika telah mulai dikembangkan. Kaum Sofis beserta Plato (427 SM-347 SM) juga telah merintis dan memberikan saran-saran dalam bidang ini.
Pada masa Aristoteles logika masih disebut dengan analitica , yang secara khusus meneliti berbagai argumentasi yang berangkat dari proposisi yang benar, dan dialektika yang secara khusus meneliti argumentasi yang berangkat dari proposisi yang masih diragukan kebenarannya. Inti dari logika Aristoteles adalah silogisme.
Buku Aristoteles to Oraganon (alat) berjumlah enam, yaitu:
1. Categoriae menguraikan pengertian-pengertian
2. De interpretatione tentang keputusan-keputusan
3. Analytica Posteriora tentang pembuktian.
4. Analytica Priora tentang Silogisme.
5. Topica tentang argumentasi dan metode berdebat.
6. De sohisticis elenchis tentang kesesatan dan kekeliruan berpikir.
Pada 370 SM - 288 SM Theophrastus, murid Aristoteles yang menjadi pemimpin Lyceum, melanjutkan pengembangn logika.
Istilah logika untuk pertama kalinya dikenalkan oleh Zeno dari Citium 334 SM - 226 SM pelopor Kaum Stoa. Sistematisasi logika terjadi pada masa Galenus (130 M - 201 M) dan Sextus Empiricus 200 M, dua orang dokter medis yang mengembangkan logika dengan menerapkan metode geometri.
Porohyus (232 - 305) membuat suatu pengantar (eisagoge) pada Categoriae, salah satu buku Aristoteles.
Boethius (480-524) menerjemahkan Eisagoge Porphyrius ke dalam bahasa Latin dan menambahkan komentar- komentarnya.
Johanes Damascenus (674 - 749) menerbitkan Fons Scienteae. Abad pertengahan dan logika modern
Masa Yunani Kuno, logika dimulai sejak Thales (624 SM - 548 SM), filsuf Yunani pertama yang meninggalkan segala dongeng, takhayul, dan cerita-cerita isapan jempol dan berpaling kepada akal budi untuk memecahkan rahasia alam semesta.
Thales mengatakan bahwa air adalah arkhe (Yunani) yang berarti prinsip atau asas utama alam semesta. Saat itu Thales telah mengenalkan logika induktif.
Aristoteles kemudian mengenalkan logika sebagai ilmu, yang kemudian disebut logica scientica. Aristoteles mengatakan bahwa Thales menarik kesimpulan bahwa air adalah arkhe alam semesta dengan alasan bahwa air adalah jiwa segala sesuatu.
Dalam logika Thales, air adalah arkhe alam semesta, yang menurut Aristoteles disimpulkan dari:
* Air adalah jiwa tumbuh-tumbuhan (karena tanpa air tumbuhan mati)
* Air adalah jiwa hewan dan jiwa manusia
* Air jugalah uap
* Air jugalah es
Jadi, air adalah jiwa dari segala sesuatu, yang berarti, air adalah arkhe alam semesta.
Sejak saat Thales sang filsuf mengenalkan pernyataannya, logika telah mulai dikembangkan. Kaum Sofis beserta Plato (427 SM-347 SM) juga telah merintis dan memberikan saran-saran dalam bidang ini.
Pada masa Aristoteles logika masih disebut dengan analitica , yang secara khusus meneliti berbagai argumentasi yang berangkat dari proposisi yang benar, dan dialektika yang secara khusus meneliti argumentasi yang berangkat dari proposisi yang masih diragukan kebenarannya. Inti dari logika Aristoteles adalah silogisme.
Buku Aristoteles to Oraganon (alat) berjumlah enam, yaitu:
1. Categoriae menguraikan pengertian-pengertian
2. De interpretatione tentang keputusan-keputusan
3. Analytica Posteriora tentang pembuktian.
4. Analytica Priora tentang Silogisme.
5. Topica tentang argumentasi dan metode berdebat.
6. De sohisticis elenchis tentang kesesatan dan kekeliruan berpikir.
Pada 370 SM - 288 SM Theophrastus, murid Aristoteles yang menjadi pemimpin Lyceum, melanjutkan pengembangn logika.
Istilah logika untuk pertama kalinya dikenalkan oleh Zeno dari Citium 334 SM - 226 SM pelopor Kaum Stoa. Sistematisasi logika terjadi pada masa Galenus (130 M - 201 M) dan Sextus Empiricus 200 M, dua orang dokter medis yang mengembangkan logika dengan menerapkan metode geometri.
Porohyus (232 - 305) membuat suatu pengantar (eisagoge) pada Categoriae, salah satu buku Aristoteles.
Boethius (480-524) menerjemahkan Eisagoge Porphyrius ke dalam bahasa Latin dan menambahkan komentar- komentarnya.
Johanes Damascenus (674 - 749) menerbitkan Fons Scienteae. Abad pertengahan dan logika modern
Pada abad 9 hingga abad 15, buku-buku Aristoteles seperti De Interpretatione, Eisagoge oleh Porphyus dan karya Boethius masih digunakan.
Thomas Aquinas 1224-1274 dan kawan-kawannya berusaha mengadakan sistematisasi logika. Lahirlah logika modern dengan tokoh-tokoh seperti:
- Petrus Hispanus (1210 - 1278)
- Roger Bacon (1214-1292)
- Raymundus Lullus (1232 -1315) yang menemukan metode logika baru yang dinamakan Ars Magna, yang merupakan semacam aljabar pengertian.
- William Ocham (1295 - 1349)
Francis Bacon (1561 - 1626) mengembangkan logika induktif yang diperkenalkan dalam bukunya Novum Organum Scientiarum.
J.S. Mills (1806 - 1873) melanjutkan logika yang menekankan pada pemikiran induksi dalam bukunya System of Logic
Lalu logika diperkaya dengan hadirnya pelopor-pelopor logika simbolik seperti:
- Gottfried Wilhelm Leibniz (1646-1716) menyusun logika aljabar berdasarkan Ars Magna dari Raymundus Lullus. Logika ini bertujuan menyederhanakan pekerjaan akal budi dan lebih mempertajam kepastian.
- George Boole (1815-1864)
- John Venn (1834-1923)
- Gottlob Frege (1848 - 1925)
Lalu Chares Sanders Peirce (1839-1914), seorang filsuf Amerika Serikat yang pernah mengajar di John Hopkins University,melengkapi logika simbolik dengan karya-karya tulisnya. Ia memperkenalkan dalil Peirce (Peirce's Law) yang menafsirkan logika selaku teori umum mengenai tanda (general theory of signs)
Puncak kejayaan logika simbolik terjadi pada tahun 1910-1913 dengan terbitnya Principia Mathematica tiga jilid yang merupakan karya bersama Alfred North Whitehead (1861 - 1914) dan Bertrand Arthur William Russel (1872 - 1970).
Logika simbolik lalu diteruskan oleh Ludwig Wittgenstein (1889-1951), Rudolf Carnap (1891-1970), Kurt Godel (1906-1978), dan lain-lain
Puncak kejayaan logika simbolik terjadi pada tahun 1910-1913 dengan terbitnya Principia Mathematica tiga jilid yang merupakan karya bersama Alfred North Whitehead (1861 - 1914) dan Bertrand Arthur William Russel (1872 - 1970).
Logika simbolik lalu diteruskan oleh Ludwig Wittgenstein (1889-1951), Rudolf Carnap (1891-1970), Kurt Godel (1906-1978), dan lain-lain
Terdapat 5 aliran besar dalam logika, yaitu :
1. Aliran Logika Tradisional
Logika ditafsirkan sebagai suatu kumpulan aturan praktis yang menjadi petunjuk pemikiran.
2. Aliran Logika Metafisis
Susunan pikiran itu dianggap kenyataan, sehingga logika dianggap seperti metafisika. Tugas pokok logika adalah menafsirkan pikiran sebagai suatu tahap dari struktur kenyataan. Sebab itu untuk mengetahui kenyataan, orang harus belajar logika lebih dahulu.
3. Aliran Logika Epistemologis
Dipelopori oleh Francis Herbert Bradley (1846 - 1924) dan Bernard Bosanquet (1848 - 1923). Untuk dapat mencapai pengetahuan yang memadai, pikiran logis dan perasaan harus digabung. Demikian juga untuk mencapai kebenaran, logika harus dihubungkan dengan seluruh pengetahuan lainnya.
4. Aliran Logika Instrumentalis (Aliran Logika Pragmatis)
Dipelopori oleh John Dewey (1859 - 1952). Logika dianggap sebagai alat (instrumen) untuk memecahkan masalah.
5. Aliran Logika Simbolis
Dipelopori oleh Leibniz, Boole dan De Morgan. Aliran ini sangat menekankan penggunaan bahasa simbol untuk mempelajari secara terinci, bagaimana akal harus bekerja. Metode-metode dalam mengembangkan matematika banyak digunakan oleh aliran ini, sehingga aliran ini berkembang sangat teknis dan ilmiah serta bercorak matematika, yang kemudian disebut Logika Matematika (Mathematical Logic). G.W. Leibniz (1646 - 1716) dianggap sebagai matematikawan pertama yang mempelajari Logika Simbolik.
Pada abad kesembilan belas, George Boole (1815 - 1864) berhasil mengembangkan Logika Simbolik. Bukunya yang berjudul Low of Though mengembangkan logika sebagai sistem matematika yang abstrak. Logika Simbolik ini merupakan logika formal yang semata-mata menelaah bentuk dan bukan isi dari apa yang dibicarakan. Ada dua pendapat tentang Logika Simbolik yang merangkum keseluruhan maknanya, yaitu
- Logika simbolik adalah ilmu tentang penyimpulan yang sah (absah), khususnya yang dikembangkan dengan penggunaan metode-metode matematika dan dengan bantuan simbol-simbol khusus sehingga memungkinkan seseorang menghindarkan makna ganda dari bahasa sehari-hari (Frederick B. Fitch dalam bukunya “Symbolic Logic”).
- Pemakaian simbol-simbol matematika untuk mewakili bahasa. Simbol-simbol itu diolah sesuai dengan aturan-aturan matematika untuk menetapkan apakah suatu pernyataan bernilai benar atau salah.
Studi tentang logika berkembang terus dan sekarang logika menjadi ilmu pengetahuan yang luas dan yang cenderung mempunyai sifat teknis dan ilmiah. Aljabar Boole, salah satu topik yang merupakan perluasan logika (dan teori himpunan), sekarang ini digunakan secara luas dalam mendesain komputer. Penggunaan simbol-simbol Boole dapat mengurangi banyak kesalahan dalam penalaran.
Ketidakjelasan berbahasa dapat dihindari dengan menggunakan simbol-simbol, karena setelah problem diterjemahkan ke dalam notasi simbolik, penyelesaiannya menjadi bersifat mekanis. Tokoh-tokoh terkenal lainnya yang menjadi pendukung perkembangan logika simbolik adalah De Morgan, Leonard Euler (1707 - 1783), John Venn (1834 - 1923), Alfred North Whitehead dan Bertrand Russell (1872 - 1970).
sejarah bilangan dalam matematika
Sejarah bilangan dapat kita telusuri dengan berbagai pendekatan. Kita dapat menyusun ulang sejarah bilangan berdasarkan solusi persamaan, yaitu persamaan linear dan persamaan kuadrat. Dengan modal bilangan asli dan persamaan linear kita akan sampai pada kesimpulan bahwa harus ada bilangan nol, sistem bilangan bulat, dan sistem bilangan rasional. Kemudian, dengan persamaan kuadrat kita akan sampai pada kesimpulan bahwa harus ada bilangan real dan bilangan kompleks.
Secara sederhana, sejarah bilangan dapat kita mulai dengan bilangan Asli. Bilangan Asli merupakan bilangan yang pertama kali dikenal manusia. Hal ini karena secara alamiah manusia akan melihat berbagai benda/objek dan kemudian untuk keperluan tertentu mereka harus menghitungnya. Mereka memiliki, uang, kambing, anak, pohon, saudara, dan lain-lain. Untuk menghitung benda-benda tersebut bilangan yang digunakan adalah bilangan Asli. Tentu saja mereka tidak menyadari bahwa bilangan yang mereka gunakan untuk menghitung tersebut adalah bilangan Asli. Penamaan tersebut dilakukan setelah jaman modern untuk keperluan pengembangan ilmu pengetahuan. Dengan demikian kita dapat mendefinisikan bahwa bilangan asli adalah bilangan yang digunakan untuk menghitung. Notasi himpunan bilangan asli adalah ℕ. Anggota bilangan asli adalah N={1,2,3,…}.
Bilangan asli yang sudah dikenal tentu harus dilengkapi dengan suatu aturan untuk mengoperasikan bilangan tersebut. Operasi tersebut adalah penjumlahan, pengurangan, perkalian, dan pembagian. Kita sudah mengetahui bahwa bilangan asli bersifat tertutup terhadap penjumlahan. Artinya, penjumlahan dua bilangan asli akan menghasilkan bilangan asli. Tetapi tidak demikian dengan pengurangan. Kita akan mendapati bahwa jika sebuah bilangan asli dikurangi dengan bilangan asli hasilnya belum tentu bilangan asli. Sebagai contoh, 5 – 5 = 0. Jelas bahwa bukan anggota bilangan asli. Oleh karena itu, sistem bilangan asli harus diperluas dengan menyertakan 0 sebagai anggota. Perluasan ini kemudian dikenal sebagai bilangan Cacah.
Bilangan nol merupakan salah satu penemuan yang sangat penting. Sebelum ada bilangan nol, menuliskan bilangan-bilangan yang besar sangat sulit. Bahkan beberapa bilangan memiliki notasi yang sama (untuk lebih lengkap, silakan baca buku Berhitung Sejarah dan Pengembangannya yang ditulis oleh Dali S. Naga). Dengan adanya bilangan nol, penulisan bilangan-bilangan yang besar pun menjadi mudah. Bilangan nol pertama kali digunakan di China dan India, tetapi kemudian dipopulerkan oleh Bangsa Arab pada era keemasan Islam.
Perkembangan selanjutnya, bilangan Cacah pun ternyata tidak dapat sepenuhnya merepresentasikan objek dalam dunia nyata. Dalam dunia nyata ada orang yang memiliki uang, ada orang yang tidak memiliki uang, dan bahkan ada orang yang memiliki utang. Keadaan pertama dapat kita tulis dengan bilangan asli, sedangkan keadaan kedua bisa kita tulis dengan bilangan 0. Bagaimana dengan keadan yang ketiga jika yang menjadi kerangka acuan adalah keberadaan uang. Hal ini akan membawa kita pada perluasan sistem bilangan cacah menjadi menjadi bilangan bulat.
Perluasan bilangan bulat dapat juga dijelaskan dengan operasi pada dua bilangan cacah. Dengan operasi pengurangan, ternyata diketahui bahwa jika dua bilangan cacah dikurangkan maka hasilnya belum tentu bilangan cacah. Sebagai contoh, 6 – 4 = 2 dan 2 masih merupakan bilangan cacah, tetapi 4 – 6 tidak ada interpretasinya dalam bilangan cacah. Selanjutnya digunakan bilangan negatif untuk menyatakan hasil 4 – 6. Dengan demikian, karena 4 – 6 merupakan kebalikan dari , maka 4 – 6 = -2. Gabungan bilangan cacah dengan bilangan negatif ini yang kemudian membentuk bilangan bulat.
Notasi himpunan bilangan bulat adalah ℤ, dan anggota bilangan bulat adalah Z={…,-3,-2,-1,0,1,2,3,…}.
Perhatikan bahwa -2 tidak hanya dihasilkan dari 4-6 , tetapi dapat juga dihasilkan dari 5 – 7, 10 – 12, 20 – 22 dan masih banyak lagi. Berdasarkan hal tersebut, setiap bilangan bulat mewakili suatu hasil pengurangan dalam cacah. Sebagai contoh, bilangan 2 mewakili hasil-hasil dari {2 – 0, 3 – 1, 4 – 2, …}. Bilangan -3 mewakili hasil-hasil dari {0 – 3, 2 – 5, 7 – 10, …}. Hal ini berarti anggota himpunan bilangan bulat adalah hasil operasi pengurangan pada bilangan asli.
Bilangan bulat yang disertai dengan operasi penjumlahan dan perkalian membentuk struktur tertentu dalam matematika. Struktur yang dimiliki bilangan bulat adalah, terhadap operasi penjumlahan, sistem bilangan bulat membentuk grup yang komutatif (grup abelian). Hal ini berarti terhadap penjumlahan bilangan bulat bersifat tertutup, asosiatif, memiliki unsur identitas, memiliki invers (lawan) dan komutatif,. Terhadap perkalian, bilangan bulat memiliki sifat, tertutup, komutatif, asosiatif, dan mempunyai unsur identitas. Dengan demikian sistem bilangan bulat memiliki sifat yang lebih lengkap daripada sistem bilangan sebelumnya.
Selanjutnya, terhadap operasi pembagian, ternyata bilangan bulat tidak bersifat tertutup. Dalam kehidupan sehari-hari kita sering harus membagi suatu objek menjadi beberapa bagian. Setelah dibagi hasilnya bisa utuh bisa juga tidak utuh. Sebagai contoh, jika kita memiliki 10 apel kemudian akan dibagikan kepada 5 anak, maka masing-masing anak akan mendapat 2 apel (masing-masing apel masih utuh). Tetapi jika 10 apel tersebut akan dibagikan kepada 20 anak, maka setiap anak mendapat setengah apel. Tidak ada bilangan bulat yang dapat digunakan untuk menyatakan hasil tersebut. Oleh karena itu, sistem bilangan diperluas.
Perluasan dari sistem bilangan bulat tersebut adalah sistem bilangan rasional. Bilangan rasional didefinisikan sebagai bilangan yang dapat ditulis sebagai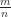 dengan m dan n bilangan bulat dan n≠0. Dengan perluasan sistem bilangan ini, maka persoalan tentang pembagian dapat diselesaikan. Jika sistem bilangan bulat membentuk struktur grup abelian terhadap operasi penjumlahan, maka sistem bilangan rasional membentuk lapangan (Field).
dengan m dan n bilangan bulat dan n≠0. Dengan perluasan sistem bilangan ini, maka persoalan tentang pembagian dapat diselesaikan. Jika sistem bilangan bulat membentuk struktur grup abelian terhadap operasi penjumlahan, maka sistem bilangan rasional membentuk lapangan (Field).
Selanjutnya, kita semua mengenal teorema Pythagoras. Jika kita mempunyai segitiga siku-siku dengan sisi tegak masing-masing 1 satuan panjang, maka panjang sisi miringnya (hypotenusa) adalah . Namun,
. Namun,  tidak dapat dinyatakan dalam bentuk m/n dengan m dan n bilangan bulat dan n≠0 (bukti lengkapnya lihat di buku analisis real). Ini berarti ada bilangan lain di luar bilangan rasional. Bilangan tersebut dikenal sebagai bilangan irasional. Gabungan bilangan rasional dan bilangan irasional membentuk sistem bilangan real. Bilangan real dapat didefinisikan sebagai bilangan yang dapat digunakan untuk mengukur. Sistem bilangan real membentuk lapangan terurut dan lengkap.
tidak dapat dinyatakan dalam bentuk m/n dengan m dan n bilangan bulat dan n≠0 (bukti lengkapnya lihat di buku analisis real). Ini berarti ada bilangan lain di luar bilangan rasional. Bilangan tersebut dikenal sebagai bilangan irasional. Gabungan bilangan rasional dan bilangan irasional membentuk sistem bilangan real. Bilangan real dapat didefinisikan sebagai bilangan yang dapat digunakan untuk mengukur. Sistem bilangan real membentuk lapangan terurut dan lengkap.
Perluasan himpunan bilangan real adalah himpunan bilangan kompleks. Kemunculan bilangan kompleks dapat diilustrasikan oleh usaha mencari solusi persamaan kuadrat . Bilangan yang memenuhi persamaan kuadrat itu adalah bilangan yang kuadratnya adalah -1. Tidak ada bilangan real yang memenuhi sifat demikian. Oleh karena itu, muncul himpunan bilangan kompleks. Himpunan bilangan kompleks dinotasikan dengan
. Bilangan yang memenuhi persamaan kuadrat itu adalah bilangan yang kuadratnya adalah -1. Tidak ada bilangan real yang memenuhi sifat demikian. Oleh karena itu, muncul himpunan bilangan kompleks. Himpunan bilangan kompleks dinotasikan dengan  dan $latex i= \sqrt{-1}} $.
dan $latex i= \sqrt{-1}} $.
Secara sederhana, sejarah bilangan dapat kita mulai dengan bilangan Asli. Bilangan Asli merupakan bilangan yang pertama kali dikenal manusia. Hal ini karena secara alamiah manusia akan melihat berbagai benda/objek dan kemudian untuk keperluan tertentu mereka harus menghitungnya. Mereka memiliki, uang, kambing, anak, pohon, saudara, dan lain-lain. Untuk menghitung benda-benda tersebut bilangan yang digunakan adalah bilangan Asli. Tentu saja mereka tidak menyadari bahwa bilangan yang mereka gunakan untuk menghitung tersebut adalah bilangan Asli. Penamaan tersebut dilakukan setelah jaman modern untuk keperluan pengembangan ilmu pengetahuan. Dengan demikian kita dapat mendefinisikan bahwa bilangan asli adalah bilangan yang digunakan untuk menghitung. Notasi himpunan bilangan asli adalah ℕ. Anggota bilangan asli adalah N={1,2,3,…}.
Bilangan asli yang sudah dikenal tentu harus dilengkapi dengan suatu aturan untuk mengoperasikan bilangan tersebut. Operasi tersebut adalah penjumlahan, pengurangan, perkalian, dan pembagian. Kita sudah mengetahui bahwa bilangan asli bersifat tertutup terhadap penjumlahan. Artinya, penjumlahan dua bilangan asli akan menghasilkan bilangan asli. Tetapi tidak demikian dengan pengurangan. Kita akan mendapati bahwa jika sebuah bilangan asli dikurangi dengan bilangan asli hasilnya belum tentu bilangan asli. Sebagai contoh, 5 – 5 = 0. Jelas bahwa bukan anggota bilangan asli. Oleh karena itu, sistem bilangan asli harus diperluas dengan menyertakan 0 sebagai anggota. Perluasan ini kemudian dikenal sebagai bilangan Cacah.
Bilangan nol merupakan salah satu penemuan yang sangat penting. Sebelum ada bilangan nol, menuliskan bilangan-bilangan yang besar sangat sulit. Bahkan beberapa bilangan memiliki notasi yang sama (untuk lebih lengkap, silakan baca buku Berhitung Sejarah dan Pengembangannya yang ditulis oleh Dali S. Naga). Dengan adanya bilangan nol, penulisan bilangan-bilangan yang besar pun menjadi mudah. Bilangan nol pertama kali digunakan di China dan India, tetapi kemudian dipopulerkan oleh Bangsa Arab pada era keemasan Islam.
Perkembangan selanjutnya, bilangan Cacah pun ternyata tidak dapat sepenuhnya merepresentasikan objek dalam dunia nyata. Dalam dunia nyata ada orang yang memiliki uang, ada orang yang tidak memiliki uang, dan bahkan ada orang yang memiliki utang. Keadaan pertama dapat kita tulis dengan bilangan asli, sedangkan keadaan kedua bisa kita tulis dengan bilangan 0. Bagaimana dengan keadan yang ketiga jika yang menjadi kerangka acuan adalah keberadaan uang. Hal ini akan membawa kita pada perluasan sistem bilangan cacah menjadi menjadi bilangan bulat.
Perluasan bilangan bulat dapat juga dijelaskan dengan operasi pada dua bilangan cacah. Dengan operasi pengurangan, ternyata diketahui bahwa jika dua bilangan cacah dikurangkan maka hasilnya belum tentu bilangan cacah. Sebagai contoh, 6 – 4 = 2 dan 2 masih merupakan bilangan cacah, tetapi 4 – 6 tidak ada interpretasinya dalam bilangan cacah. Selanjutnya digunakan bilangan negatif untuk menyatakan hasil 4 – 6. Dengan demikian, karena 4 – 6 merupakan kebalikan dari , maka 4 – 6 = -2. Gabungan bilangan cacah dengan bilangan negatif ini yang kemudian membentuk bilangan bulat.
Notasi himpunan bilangan bulat adalah ℤ, dan anggota bilangan bulat adalah Z={…,-3,-2,-1,0,1,2,3,…}.
Perhatikan bahwa -2 tidak hanya dihasilkan dari 4-6 , tetapi dapat juga dihasilkan dari 5 – 7, 10 – 12, 20 – 22 dan masih banyak lagi. Berdasarkan hal tersebut, setiap bilangan bulat mewakili suatu hasil pengurangan dalam cacah. Sebagai contoh, bilangan 2 mewakili hasil-hasil dari {2 – 0, 3 – 1, 4 – 2, …}. Bilangan -3 mewakili hasil-hasil dari {0 – 3, 2 – 5, 7 – 10, …}. Hal ini berarti anggota himpunan bilangan bulat adalah hasil operasi pengurangan pada bilangan asli.
Bilangan bulat yang disertai dengan operasi penjumlahan dan perkalian membentuk struktur tertentu dalam matematika. Struktur yang dimiliki bilangan bulat adalah, terhadap operasi penjumlahan, sistem bilangan bulat membentuk grup yang komutatif (grup abelian). Hal ini berarti terhadap penjumlahan bilangan bulat bersifat tertutup, asosiatif, memiliki unsur identitas, memiliki invers (lawan) dan komutatif,. Terhadap perkalian, bilangan bulat memiliki sifat, tertutup, komutatif, asosiatif, dan mempunyai unsur identitas. Dengan demikian sistem bilangan bulat memiliki sifat yang lebih lengkap daripada sistem bilangan sebelumnya.
Selanjutnya, terhadap operasi pembagian, ternyata bilangan bulat tidak bersifat tertutup. Dalam kehidupan sehari-hari kita sering harus membagi suatu objek menjadi beberapa bagian. Setelah dibagi hasilnya bisa utuh bisa juga tidak utuh. Sebagai contoh, jika kita memiliki 10 apel kemudian akan dibagikan kepada 5 anak, maka masing-masing anak akan mendapat 2 apel (masing-masing apel masih utuh). Tetapi jika 10 apel tersebut akan dibagikan kepada 20 anak, maka setiap anak mendapat setengah apel. Tidak ada bilangan bulat yang dapat digunakan untuk menyatakan hasil tersebut. Oleh karena itu, sistem bilangan diperluas.
Perluasan dari sistem bilangan bulat tersebut adalah sistem bilangan rasional. Bilangan rasional didefinisikan sebagai bilangan yang dapat ditulis sebagai
Selanjutnya, kita semua mengenal teorema Pythagoras. Jika kita mempunyai segitiga siku-siku dengan sisi tegak masing-masing 1 satuan panjang, maka panjang sisi miringnya (hypotenusa) adalah
Perluasan himpunan bilangan real adalah himpunan bilangan kompleks. Kemunculan bilangan kompleks dapat diilustrasikan oleh usaha mencari solusi persamaan kuadrat
Langganan:
Komentar (Atom)